Antiderivative Calculator With Steps
Antiderivative calculator finds the antiderivative of a function step by step with respect to a variable i.e., x, y, or z. This online integration calculator also supports upper bound and lower bound in case you are working with minimum or maximum value of intervals.
With this integral calculator, you can get step-by-step calculations of:
Definite integral
Indefinite integral
It can find the integrals of logarithmic as well as trigonometric functions. This tool assesses the input function and uses integral rules accordingly to evaluate the integrals for the area, volume, etc.
How does this antiderivative calculator work?
You can find the antiderivative (integral) of any function by following the steps below.
- Select the definite or indefinite option.
- Enter the function in the given input box.
- Specify the variable. It is set as x by default.
- Enter the Upper and Lower bound limit if you chose the definite integral above.
- Hit the Calculate button. You will get the result with step-by-step calculations.
- Press the clear button to recalculate.
- Click the Load Example button if you want to use a sample example.
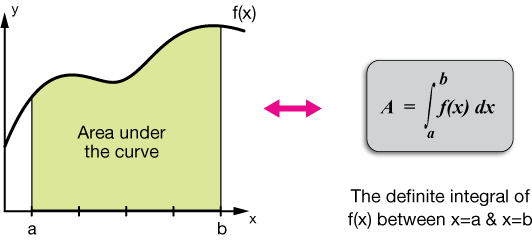
What is an Integral?
An integral can be defined as,
“Integral assigns numbers to functions in a way that describes volume, area, displacement, and other ideas that arise by combining infinitesimal data.”
The process of finding integrals is called integration. Integral is also referred to as antiderivative because it is a reverse operation of derivation.
Along with differentiation, integration is an essential operation of calculus and serves as a tool to solve problems in mathematics and physics involving the length of a curve, the volume of a solid, and the area of an arbitrary shape among others.
The integral of a function f(x) with respect to a real variable x on an interval [a, b] is written as:
\(\int _a^bf\left(x\right)dx\:\)
How to find Antiderivative (Integral)?
See the below examples to learn how to evaluate definite and indefinite integrals using rules of integration.
Example # 1
Definite Integral
Evaluate \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Solution:
- Apply the sum rule. Write the integration sign with each variable separately.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
The above function can be written as:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Apply the power rule on both expressions to evaluate the exponents.
Power Rule: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(=\:\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(=\:\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Apply the constant rule which leaves C with the final expression.
Constant Rule:
\(=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(=\frac{2}{3}+\frac{3}{4}\)
\(=\frac{17}{12}=1.4167\)
Example # 2
Indefinite integral
Evaluate \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Solution:
- Rearrange the function as below.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Apply the sum rule to the function.
Sum Rule: \(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ... Equ. 1
- Solve each expression in the above function by implementing integral rules.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ------- d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\) ------- Power rule applied.
\(\int xdx=\frac{x^2}{2}\:\) ------- Power rule applied. Refer to the previous example
- Substitute the solve values in Equation 1.
\(=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\)
\(=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C is added because of the constant rule.
- Simplify the equation if needed.
\(=-2cos\left(x\right)+x^3−3x^2+C\)
FAQs
What is the integral of 1/x?
The integral of 1/x is an absolute value: ln (|x|) + C. It is a standard integration value.
What is the difference between definite and indefinite integral?
A definite integral denotes a number when the upper and lower bounds are constants. On the other hand, the indefinite integral is a family of functions whose derivatives are f. The difference between the two functions is a constant.
What is the antiderivative of tan(x) dx?
The antiderivative of tan(x) dx is,
tan x = - ln |cos x| + C
What is the antiderivative of 1/x^2 dx?
-1/x + C is the antiderivative of 1/x^2