Table of Contents
ステップ付きの不定積分計算機
不定積分計算機は、変数(x、y、またはz)に関して、関数の不定積分を段階的に検出します。このオンライン統合計算機は、間隔の最小値または最大値で作業している場合の上限と下限もサポートします。
この積分計算機を使用すると、次のステップバイステップの計算を取得できます。
定積分
不定積分
対数関数と三角関数の積分を見つけることができます。このツールは入力関数を評価し、それに応じて積分ルールを使用して、面積、体積などの積分を評価します。
不定積分計算機はどのように機能しますか?
このツールは、指定された関数を分析してツリーに変換するパーサーを使用します。コンピューターはツリーを解釈して操作の順序を正しく評価し、統合ルールを適切に実装します。
以下の手順に従うことで、任意の関数の不定積分(積分)を見つけることができます。
- 確定または不確定のオプションを選択します。
- 所定の入力ボックスに関数を入力します。
- サンプル例を使用する場合は、[例のロード]ボタンをクリックします。
- 変数を指定します。デフォルトではxに設定されています。
- 上記で定積分を選択した場合は、上限と下限を入力します。
- [計算]ボタンをクリックします。ステップバイステップの計算で結果が得られます。
アイコンをクリックすると、ソリューションをダウンロードできます。
インテグラルとは何ですか?
積分は次のように定義できます。
インテグラルは、体積、面積、変位、および微小データを組み合わせることによって生じるその他のアイデアを説明する方法で、関数に数値を割り当てます。
積分を見つけるプロセスは、積分と呼ばれます。積分は、微分の逆演算であるため、不定積分とも呼ばれます。
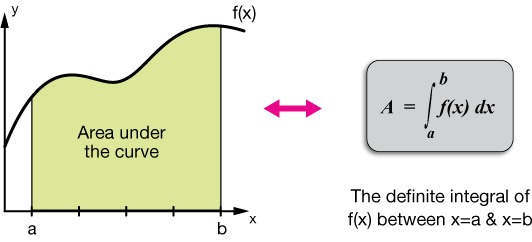
微分に加えて、積分は微積分の重要な操作であり、曲線の長さ、立体の体積、任意の形状の面積など、数学や物理学の問題を解決するためのツールとして機能します。
区間[a、b]の実変数xに関する関数f(x)の積分は、次のように記述されます。
\(\int _a^bf\left(x\right)dx\:\)
不定積分(積分)を見つける方法は?
積分の規則を使用して定積分と不定積分を評価する方法については、以下の例を参照してください。
例1
定積分
評価 \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
解決:
- 合計ルールを適用します。各変数で積分記号を個別に記述します。
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
上記の関数は次のように書くことができます:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- 指数を評価するには、両方の式にべき乗則を適用します。
べき乗則: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Cに最終式を残す定数ルールを適用します。
一定のルール:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
例2
不定積分
評価 \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
解決:
- 以下のように機能を並べ替えます。
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- 関数に合計ルールを適用します。
合計ルール: \(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ...式1
- 積分規則を実装して、上記の関数の各式を解きます。
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- 式1のソルブ値を代入します。
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
定数ルールのためにCが追加されます。
- 必要に応じて方程式を単純化します。
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
よくある質問
1 / xの積分は何ですか?
1 / xの積分は絶対値です:ln(| x |)+C。これは標準の積分値です。
確定積分と不定積分の違いは何ですか?
定積分は、上限と下限が定数の場合の数値を示します。一方、不定積分は、導関数がfである関数のファミリーです。 2つの関数の違いは定数です。
tan(x)dxの不定積分は何ですか?
tan(x)dxの不定積分は、
tan x = --ln | cos x | + C