Table of Contents
Калькулятор первообразных с шагами
Калькулятор первообразной находит первообразную функции шаг за шагом по переменной, т. е. x, y или z. Этот онлайн-калькулятор интеграции также поддерживает верхнюю и нижнюю границы, если вы работаете с минимальным или максимальным значением интервалов.
С помощью этого интегрального калькулятора вы можете получить пошаговые расчеты:
- Определенный интеграл
- Неопределенный интеграл
Он может найти интегралы логарифмических, а также тригонометрических функций. Этот инструмент оценивает входную функцию и соответственно использует интегральные правила для вычисления интегралов для площади, объема и т. д.
Как работает антипроизводный калькулятор?
Этот инструмент использует синтаксический анализатор, который анализирует заданную функцию и преобразует ее в дерево. Компьютер интерпретирует дерево для правильной оценки порядка операций и соответствующим образом реализует правила интеграции.
Вы можете найти первообразную (интеграл) любой функции, выполнив следующие действия.
- Выберите определенный или неопределенный вариант.
- Введите функцию в данное поле ввода.
- Нажмите кнопку «Загрузить пример», если вы хотите использовать образец примера.
- Укажите переменную. По умолчанию он установлен как x.
- Введите верхнюю и нижнюю границы, если вы выбрали определенный интеграл выше.
- Нажмите кнопку "Рассчитать". Вы получите результат с пошаговыми расчетами.
Вы можете скачать решение, нажав на иконку.
Что такое интеграл?
Интеграл можно определить как
«Integral присваивает числа функциям таким образом, который описывает объем, площадь, перемещение и другие идеи, возникающие при объединении бесконечно малых данных».
Процесс нахождения интегралов называется интегрированием. Интеграл также называют первообразной, потому что это обратная операция вывода.
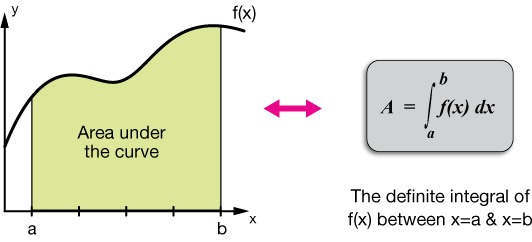
Наряду с дифференцированием интегрирование является важной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных с длиной кривой, объемом твердого тела и площадью произвольной формы среди других.
Интеграл функции f(x) по действительной переменной x на интервале [a, b] записывается как:
\(\int _a^bf\left(x\right)dx\:\)
Как найти первообразную (интеграл)?
См. приведенные ниже примеры, чтобы узнать, как вычислять определенные и неопределенные интегралы, используя правила интегрирования.
Пример №1
Определенный интеграл
Оценивать \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Решение:
- Примените правило сумм. Запишите знак интегрирования с каждой переменной отдельно.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
Вышеупомянутая функция может быть записана как:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Примените степенное правило к обоим выражениям, чтобы вычислить показатели степени.
Правило питания: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Примените постоянное правило, которое оставляет C с окончательным выражением.
Постоянное правило:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Пример №2
Неопределенный интеграл
Оценивать \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Решение:
- Переставьте функцию, как показано ниже.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Примените правило сумм к функции.
Правило суммы:
\(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ...Уравнение 1
- Решите каждое выражение в приведенной выше функции, реализуя интегральные правила.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Подставьте значения решения в уравнение 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C добавлен из-за постоянного правила.
- Упростите уравнение, если это необходимо.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
Часто задаваемые вопросы
Чему равен интеграл от 1/x?
Интеграл от 1/x представляет собой абсолютное значение: ln (|x|) + C. Это стандартное значение интегрирования.
Чем отличается определенный интеграл от неопределенного?
Определенный интеграл обозначает число, когда верхняя и нижняя границы являются постоянными. С другой стороны, неопределенный интеграл – это семейство функций, производная которых равна f. Разница между двумя функциями является константой.
Что такое первообразная tan(x) dx?
Первообразная tan(x) dx равна,
тангенс x = - ln |cos x| + С