Inhaltsverzeichnis
Stammfunktion Rechner mit Schritten
Der stammfunktion rechner findet Schritt für Schritt die Stammfunktion einer Funktion in Bezug auf eine Variable, z. B. x, y oder z. Dieser Online-Integrationsrechner unterstützt auch Obergrenzen und Untergrenzen, falls Sie mit dem Mindest- oder Höchstwert von Intervallen arbeiten.
Mit diesem Integralrechner erhalten Sie Schritt-für-Schritt-Berechnungen von:
- Bestimmtes Integral
- Unbestimmtes Integral
Es kann die Integrale von logarithmischen sowie trigonometrischen Funktionen finden. Dieses Tool bewertet die Eingabefunktion und verwendet entsprechende Integralregeln, um die Integrale für die Fläche, das Volumen usw. auszuwerten.
Wie funktioniert der Stammfunktionsrechner?
Dieses Tool verwendet einen Parser, der die angegebene Funktion analysiert und in einen Baum umwandelt. Der Computer interpretiert den Baum, um die Reihenfolge der Operationen korrekt auszuwerten, und implementiert die Integrationsregeln entsprechend.
Du kannst die Stammfunktion (Integral) jeder Funktion finden, indem du die folgenden Schritte befolgst.
- Wählen Sie die Option „bestimmt“ oder „unbestimmt“ aus.
- Geben Sie die Funktion in das vorgegebene Eingabefeld ein.
- Klicken Sie auf die Schaltfläche Beispiel laden, wenn Sie ein Beispielbeispiel verwenden möchten.
- Geben Sie die Variable an. Es ist standardmäßig auf x gesetzt.
- Geben Sie die Ober- und Untergrenze ein, wenn Sie oben definitives Integral gewählt haben.
- Klicken Sie auf die Schaltfläche „Berechnen“. Sie erhalten das Ergebnis mit Schritt-für-Schritt-Berechnungen.
Sie können die Lösung herunterladen, indem Sie auf das Symbol klicken.
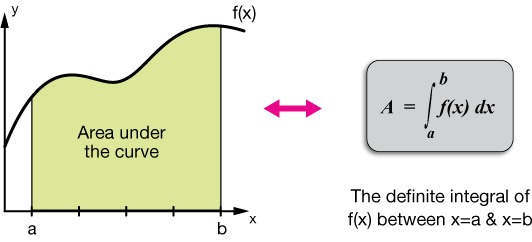
Was ist ein Integral?
Ein Integral definiert werden als,
"Integral ordnet Funktionen Zahlen auf eine Weise zu, die Volumen, Fläche, Verschiebung und andere Ideen beschreibt, die durch die Kombination von unendlich kleinen Daten entstehen."
Der Prozess des Findens von Integralen wird Integration genannt. Integral wird auch Stammfunktion genannt, weil es eine umgekehrte Operation der Ableitung ist.
Zusammen mit der Differenzierung ist die Integration eine wesentliche Operation der Analysis und dient als Werkzeug zur Lösung von Problemen in Mathematik und Physik, die unter anderem die Länge einer Kurve, das Volumen eines Festkörpers und die Fläche einer beliebigen Form betreffen.
Das Integral einer Funktion f(x) in Bezug auf eine reelle Variable x auf einem Intervall [a, b] wird geschrieben als:
\(\int _a^bf\left(x\right)dx\:\)
Wie finde ich die Stammfunktion (Integral)?
Sehen Sie sich die folgenden Beispiele an, um zu lernen, wie bestimmte und unbestimmte Integrale mithilfe von Integrationsregeln ausgewertet werden.
Beispiel 1
Bestimmtes Integral
Auswerten Valutare \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Lösung:
1.Wende die Summenregel an. Schreiben Sie das Integrationszeichen für jede Variable separat.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
Die obige Funktion kann geschrieben werden als:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Wenden Sie die Potenzregel auf beide Ausdrücke an, um die Exponenten auszuwerten.
Machtregel:
\(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
3.Wenden Sie eine Konstantenregel an, die C mit dem endgültigen Ausdruck belässt.
Konstante Regel:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Beispiel Nr. 2
Unbestimmtes Integral
Auswerten \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Lösung:
1.Ordnen Sie die Funktion wie unten beschrieben neu an.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
2.Summenregel auf die Funktion anwenden.
Summenregel:
\(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) vergelijking 1
- Los elke uitdrukking in de bovenstaande functie op door integrale regels te implementeren.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Vervang de oploswaarden in vergelijking 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C wordt toegevoegd vanwege de constante regel.
- Vereenvoudig de vergelijking indien nodig.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
Veelgestelde vragen
Wat is de integraal van 1/x?
De integraal van 1/x is een absolute waarde: ln (|x|) + C. Het is een standaard integratiewaarde.
Wat is het verschil tussen bepaalde en onbepaalde integraal?
Een bepaalde integraal geeft een getal aan wanneer de boven- en ondergrenzen constanten zijn. Aan de andere kant is de onbepaalde integraal een familie van functies waarvan de afgeleide f is. Het verschil tussen de twee functies is een constante.
Wat is het antiderivaat van tan(x) dx?
Het primitieve van tan(x) dx is,
tan x = - ln |cos x| + C