Table of Contents
Calculateur de primitive avec étapes
Calculateur de primitive trouve la primitive d'une fonction pas à pas par rapport à une variable, c'est-à-dire x, y ou z. Cette calculatrice d'intégration en ligne prend également en charge la limite supérieure et la limite inférieure si vous travaillez avec une valeur minimale ou maximale d'intervalles.
Avec cette calculatrice intégrale, vous pouvez obtenir des calculs étape par étape de :
- Intégrale définie
- Intégrale indéfinie
Il peut trouver les intégrales des fonctions logarithmiques et trigonométriques. Cet outil évalue la fonction d'entrée et utilise des règles intégrales en conséquence pour évaluer les intégrales pour la surface, le volume, etc.
Comment fonctionne la calculatrice primitive?
Cet outil utilise un analyseur qui analyse la fonction donnée et la convertit en arbre. L'ordinateur interprète l'arbre pour évaluer correctement l'ordre des opérations et implémente les règles d'intégration de manière appropriée.
Vous pouvez trouver la primitive (intégrale) de n'importe quelle fonction en suivant les étapes ci-dessous.
- Sélectionnez l'option définie ou indéfinie.
- Entrez la fonction dans la zone de saisie donnée.
- Cliquez sur le bouton Charger l'exemple si vous souhaitez utiliser un exemple d'exemple.
- Spécifiez la variable. Il est défini sur x par défaut.
- Saisissez les limites supérieure et inférieure si vous avez choisi l'intégrale définie ci-dessus.
- Appuyez sur le bouton Calculer. Vous obtiendrez le résultat avec des calculs étape par étape.
Vous pouvez télécharger la solution en cliquant sur l'icône.
Qu'est-ce qu'une intégrale?
Une intégrale peut être définie comme,
"L'intégrale attribue des nombres aux fonctions d'une manière qui décrit le volume, la surface, le déplacement et d'autres idées qui surgissent en combinant des données infinitésimales."
Le processus de recherche d'intégrales s'appelle l'intégration. L'intégrale est également appelée antidérivée car il s'agit d'une opération inverse de dérivation.
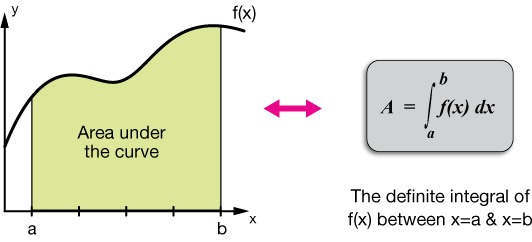
Avec la différenciation, l'intégration est une opération essentielle du calcul et sert d'outil pour résoudre des problèmes de mathématiques et de physique impliquant la longueur d'une courbe, le volume d'un solide et l'aire d'une forme arbitraire, entre autres.
L'intégrale d'une fonction f(x) par rapport à une variable réelle x sur un intervalle [a, b] s'écrit:
\(\int _a^bf\left(x\right)dx\:\)
Exemple 1
Intégrale définie
Évaluer \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Solution:
- Appliquez la règle de la somme. Écrivez le signe d'intégration avec chaque variable séparément.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
La fonction ci-dessus peut s'écrire:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Appliquez la règle de puissance sur les deux expressions pour évaluer les exposants.
Règle de puissance: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Appliquer la règle constante qui laisse C avec l'expression finale.
Règle constante:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Exemple # 2
Intégrale indéfinie
Évaluer \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Solution:
- Réorganisez la fonction comme ci-dessous.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Appliquer la règle de somme à la fonction.
Règle de somme:
\(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) Équation 1
- Résolvez chaque expression de la fonction ci-dessus en implémentant des règles intégrales.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Remplacez les valeurs de résolution dans l'équation 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C est ajouté en raison de la règle constante.
- Simplifiez l'équation si nécessaire.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
FAQ
Quelle est l'intégrale de 1/x?
L'intégrale de 1/x est une valeur absolue : ln (|x|) + C. C'est une valeur d'intégration standard.
Quelle est la différence entre intégrale définie et indéfinie?
Une intégrale définie désigne un nombre lorsque les limites supérieure et inférieure sont des constantes. D'autre part, l'intégrale indéfinie est une famille de fonctions dont les dérivées sont f. La différence entre les deux fonctions est une constante.
Quelle est la primitive de tan(x) dx?
La primitive de tan(x) dx est,
tan x = - ln |cos x| +C