Table of Contents
Calcolatrice antiderivativa con passaggi
La calcolatrice antiderivativa trova l'antiderivata di una funzione passo dopo passo rispetto a una variabile, ad esempio x, y o z. Questo calcolatore di integrazione online supporta anche il limite superiore e inferiore nel caso in cui lavori con il valore minimo o massimo degli intervalli.
Con questo calcolatore integrale, puoi ottenere calcoli passo dopo passo di:
- Integrale definito
- Integrale indefinito
Può trovare gli integrali di funzioni logaritmiche e trigonometriche. Questo strumento valuta la funzione di input e utilizza le regole integrali di conseguenza per valutare gli integrali per l'area, il volume, ecc.
Come funziona il calcolatore antiderivate?
Questo strumento utilizza un parser che analizza la funzione data e la converte in un albero. Il computer interpreta l'albero per valutare correttamente l'ordine delle operazioni e implementa le regole di integrazione in modo appropriato.
Puoi trovare l'antiderivativa (integrale) di qualsiasi funzione seguendo i passaggi seguenti.
- Seleziona l'opzione definita o indefinita.
- Immettere la funzione nella casella di input indicata.
- Fare clic sul pulsante Carica esempio se si desidera utilizzare un esempio di esempio.
- Specificare la variabile. È impostato come x per impostazione predefinita.
- Inserisci il limite superiore e inferiore se hai scelto l'integrale definito sopra.
- Premi il pulsante Calcola. Otterrai il risultato con calcoli passo dopo passo.
Puoi scaricare la soluzione cliccando sull'icona.
Che cos'è un integrale?
Un integrale può essere definito come
"Integral assegna numeri alle funzioni in un modo che descrive volume, area, spostamento e altre idee che sorgono combinando dati infinitesimali".
Il processo di ricerca degli integrali è chiamato integrazione. Integrale è anche indicato come antiderivato perché è un'operazione inversa di derivazione.
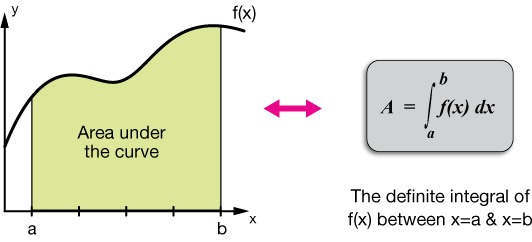
Insieme alla differenziazione, l'integrazione è un'operazione essenziale del calcolo e serve come strumento per risolvere problemi di matematica e fisica che coinvolgono, tra gli altri, la lunghezza di una curva, il volume di un solido e l'area di una forma arbitraria.
L'integrale di una funzione f(x) rispetto a una variabile reale x su un intervallo [a, b] è scritto come:
\(\int _a^bf\left(x\right)dx\:\)
Come trovare l'antiderivato (integrale)?
Vedere gli esempi seguenti per imparare a valutare integrali definiti e indefiniti utilizzando regole di integrazione.
Esempio 1
Integrale definito
Valutare \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Soluzione:
- Applicare la regola della somma. Scrivi il segno di integrazione con ciascuna variabile separatamente.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
La funzione di cui sopra può essere scritta come:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Applicare la regola di potenza su entrambe le espressioni per valutare gli esponenti.
Regola del potere: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Applicare la regola costante che lascia C con l'espressione finale.
Regola costante:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Esempio n. 2
Integrale indefinito
Valutare \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Soluzione:
- Riorganizzare la funzione come di seguito.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Applicare la regola della somma alla funzione.
Regola somma: \(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ...Ecuación 1
- Risolvi ogni espressione nella funzione precedente implementando regole integrali.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Sostituisci i valori di soluzione nell'equazione 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C viene aggiunto a causa della regola costante.
- Se necessario, semplifica l'equazione.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
Domande frequenti
Qual è l'integrale di 1/x?
L'integrale di 1/x è un valore assoluto: ln (|x|) + C. È un valore di integrazione standard.
Qual è la differenza tra integrale definito e indefinito?
Un integrale definito denota un numero quando i limiti superiore e inferiore sono costanti.
D'altra parte, l'integrale indefinito è una famiglia di funzioni la cui derivata sono f. La differenza tra le due funzioni è una costante.
Qual è l'antiderivata di tan(x) dx?
L'antiderivata di tan(x) dx è,
tan x = - ln |cos x| + C