Table of Contents
Adımlı integral hesap makinesi
Integral hesaplayıcı, x, y veya z gibi bir değişkene göre bir fonksiyonun ters türevini adım adım bulur. Bu çevrimiçi entegrasyon hesaplayıcı, minimum veya maksimum aralık değeriyle çalışıyorsanız, üst sınırı ve alt sınırı da destekler.
Bu integral hesaplayıcı ile aşağıdakilerin adım adım hesaplamalarını alabilirsiniz:
- Kesin integral
- belirsiz integral
Logaritmik ve trigonometrik fonksiyonların integrallerini bulabilir. Bu araç, girdi işlevini değerlendirir ve alan, hacim vb. için integralleri değerlendirmek için buna göre integral kurallarını kullanır.\
Integral hesaplama nasıl çalışır?
Bu araç, verilen işlevi analiz eden ve onu bir ağaca dönüştüren bir ayrıştırıcı kullanır. Bilgisayar, işlem sırasını doğru bir şekilde değerlendirmek için ağacı yorumlar ve entegrasyon kurallarını uygun şekilde uygular.
Aşağıdaki adımları izleyerek herhangi bir fonksiyonun ters türevini (integralini) bulabilirsiniz.
- Kesin veya belirsiz seçeneğini belirleyin.
- Verilen giriş kutusuna işlevi girin.
- Örnek bir örnek kullanmak istiyorsanız, Örnek Yükle düğmesini tıklayın.
- Değişkeni belirtin. Varsayılan olarak x olarak ayarlanmıştır.
- Yukarıda kesin integrali seçtiyseniz Üst ve Alt sınır sınırını girin.
- Hesapla düğmesine basın. Adım adım hesaplamalarla sonuca ulaşacaksınız.
Çözümü ikona tıklayarak indirebilirsiniz.
İntegral nedir?
Bir integral şu şekilde tanımlanabilir,
"İntegral, sonsuz küçük verileri birleştirerek ortaya çıkan hacim, alan, yer değiştirme ve diğer fikirleri açıklayacak şekilde fonksiyonlara sayılar atar."
İntegral bulma sürecine entegrasyon denir. İntegral, türetmenin ters bir işlemi olduğu için ters türev olarak da adlandırılır.
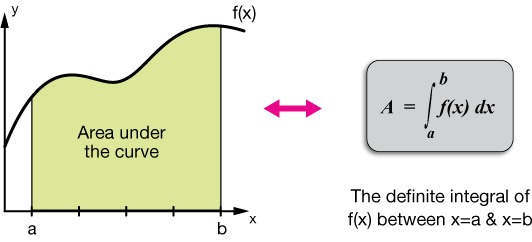
Farklılaşmanın yanı sıra entegrasyon, kalkülüsün temel bir işlemidir ve matematik ve fizikteki bir eğrinin uzunluğunu, bir katının hacmini ve diğerlerinin yanı sıra rastgele bir şeklin alanını içeren problemleri çözmek için bir araç olarak hizmet eder.
Bir f(x) işlevinin [a, b] aralığındaki x gerçek değişkenine göre integrali şu şekilde yazılır:
\(\int _a^bf\left(x\right)dx\:\)
Ters türev (İntegral) nasıl bulunur?
Entegrasyon kurallarını kullanarak belirli ve belirsiz integralleri nasıl değerlendireceğinizi öğrenmek için aşağıdaki örneklere bakın.
Örnek 1
Kesin integral
Değerlendirmek \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Çözüm:
- Toplam kuralını uygulayın. İntegrasyon işaretini her değişkenle ayrı ayrı yazın.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
Yukarıdaki fonksiyon şu şekilde yazılabilir:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Üsleri değerlendirmek için her iki ifadeye de güç kuralı uygulayın.
Güç Kuralı: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- C'yi son ifadeyle bırakan sabit kuralı uygulayın.
Sabit Kural:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Örnek # 2
belirsiz integral
Değerlendirmek \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Çözüm:
Fonksiyonu aşağıdaki gibi yeniden düzenleyin.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
Fonksiyona toplam kuralı uygulayın.
Toplam Kuralı:
\(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ... denklem 1
- İntegral kurallarını uygulayarak yukarıdaki fonksiyondaki her ifadeyi çözün.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Denklem 1'deki çözme değerlerini değiştirin.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
Sabit kuralı nedeniyle C eklenir.
- Gerekirse denklemi basitleştirin.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
SSS
1/x'in integrali nedir?
1/x'in integrali mutlak bir değerdir: ln (|x|) + C. Standart bir integral değeridir.
Belirli ve belirsiz integral arasındaki fark nedir?
Belirli bir integral, üst ve alt sınırlar sabit olduğunda bir sayıyı belirtir. Öte yandan, belirsiz integral, türevi f olan bir fonksiyon ailesidir. İki fonksiyon arasındaki fark bir sabittir.
tan(x) dx'in ters türevi nedir?
tan(x) dx'in ters türevi,
tan x = - ln |cos x| + C